引言

嘿，悄咪咪的问你个问题，你觉得整数平方一定大于零吗？
（那不然呢，整数的平方还能小于零不成）
哎，别急着回答
我们先来跑一段C语言代码来看看：

int sq(int x)
{
    return x*x;
}

int main(int argc, char *argv[])
{
    int i;
    for (i = 1; i < argc; i++) {
	int x = atoi(argv[i]);
	int sx = sq(x);
	printf("sq(%d) = %d\n", x, sx);
    }
    return 0;
}

这段代码主要是实现输入一个整数然后输出它的平方
运行结果如下：

./sq 3
sq(3) = 9
./sq 30000
sq(30000) = 900000000
./sq 50000
sq(50000) = -1794967296

最后一个结果居然是：sq(50000) = -1794967296
（咦？这个五万的平方为什么会是个负数？？？）
（明明前面的结果是正确的，为什么到这里画风就突然说变就变了？）

过程

让我们先来看一个表格

类型	储大小	值范围
char	1 字节	-128 到 127 或 0 到 255
unsigned char	1 字节	0 到 255
signed char	1 字节	-128 到 127
int	2 或 4 字节	-32,768 到 32,767 或 -2,147,483,648 到 2,147,483,647
unsigned int	2 或 4 字节	0 到 65,535 或 0 到 4,294,967,295
short	2 字节	-32,768 到 32,767
unsigned short	2 字节	0 到 65,535
long	4 字节	-2,147,483,648 到 2,147,483,647
unsigned long	4 字节	0 到 4,294,967,295

在表格中我们可以看到，(int)型数据最多只能把 大于等于 -2,147,483,648且小于等于 2,147,483,647 的数字储存在计算机里面。
但为什么会这样呢？
因为在计算机内部，无论任何数据，都是以二进制，也就是0和1来储存的

一个0或是一个1就占据了一个比特（bit）
而通过下面的转换后就变成了我们所熟悉的MB、GB等单位

1B(Byte) = 8bit;
1KB = 1024B(Byte);
1MB = 1024KB(Byte);
1 GB = 1024 MB;

再看刚才的表格， (int)型数据是以4个字节(Byte)的大小、二进制的形式储存在我们的计算机里面，而4个字节 = 32比特。int型数据就是以二进制补码的形式储存在我们的计算机里面。

理论上4个字节的零一序列能够表示的最大的数是：
2^32 - 1 = 4,294,967,295
但在这一串零一序列中，它的最高位充当了符号位，符号位为0表示该数为正，符号位为1则表示该数位负，所以真正影响数字大小的是这个符号位后面的31个比特的零一序列，所以 (int)型数据的范围就是从-2,147,483,648到2,147,483,647。
在了解到这些后，我们在反过头来看代码的运行结果：
当运算3 x 3的时候

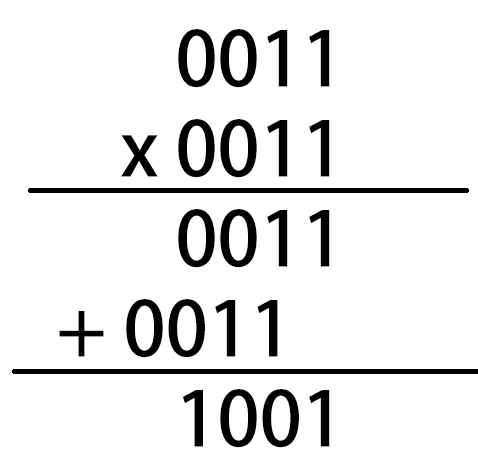
十进制的3用二进制表示就是11，3的平方是9，用二进制表示是1001。
3的平方运算的结果仅用4个比特就可以表示，相较于int型数据所拥有的31个能够确切表示数字的比特位来说，运算3的平方是绝不会超出它的范围的。
但是当我们运算5万的平方的时候它又发生了什么呢？请看下图：

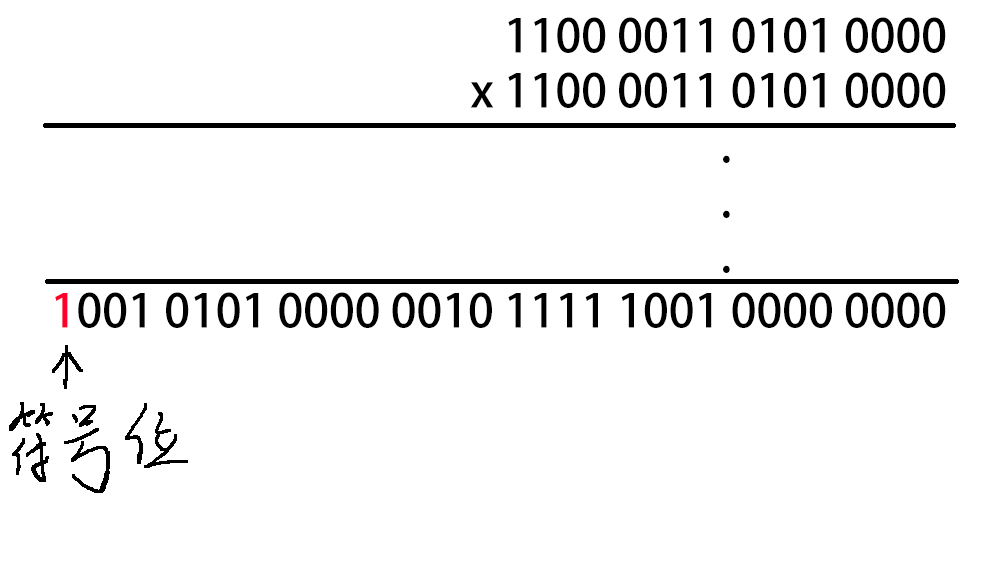
5万用二进制表示是
1100 0011 0101 0000
它平方的结果用二进制表示是
1001 0101 0000 0010 1111 1001 0000 0000

由于int型数据最多只有32个比特位可以用来储存数据，所以恰好能够把五万的平方的运算结果储存进去。
但是，能够用于精确表示数字的只有后面的31个比特位。
并且，在五万的平方的二进制表示中，它的最高位为1，这就意味着计算机会把它当成一个负数来进行读取，从而展现在我们面前的就是一个负数，而不是一个正数。

结尾

最后，回到我们刚刚开始的问题：整数平方一定大于零吗？

或许，在自然界中，上述命题肯定是成立的，但是放在计算机的世界就不一样了。我们应加深自己对计算机的了解，一些在自然界的真命题遇到计算机后就不一定的，我们在编写代码的时候，应该时时刻刻注意这些与我们日常认识不一样的地方，才能够使我们的代码更为健壮。