预测
简介
无人车需要在许多物体之间穿梭,为了保证能够做出最佳的决策,需要对这些物体的运动路径进行预测,为决策提供必要信息。
路径预测的两个要求:
- 实时性
- 指的是算法的延迟越短越好
- 准确性
- 尽可能准确的预测才能帮助无人车做出更好的决策
预测模型你应该能够学习新的行为,因为开发出每种场景的静态模型是一个不太可能完成得了的任务。
不同的预测方式
为了预测一辆汽车是要直行还是要左转?
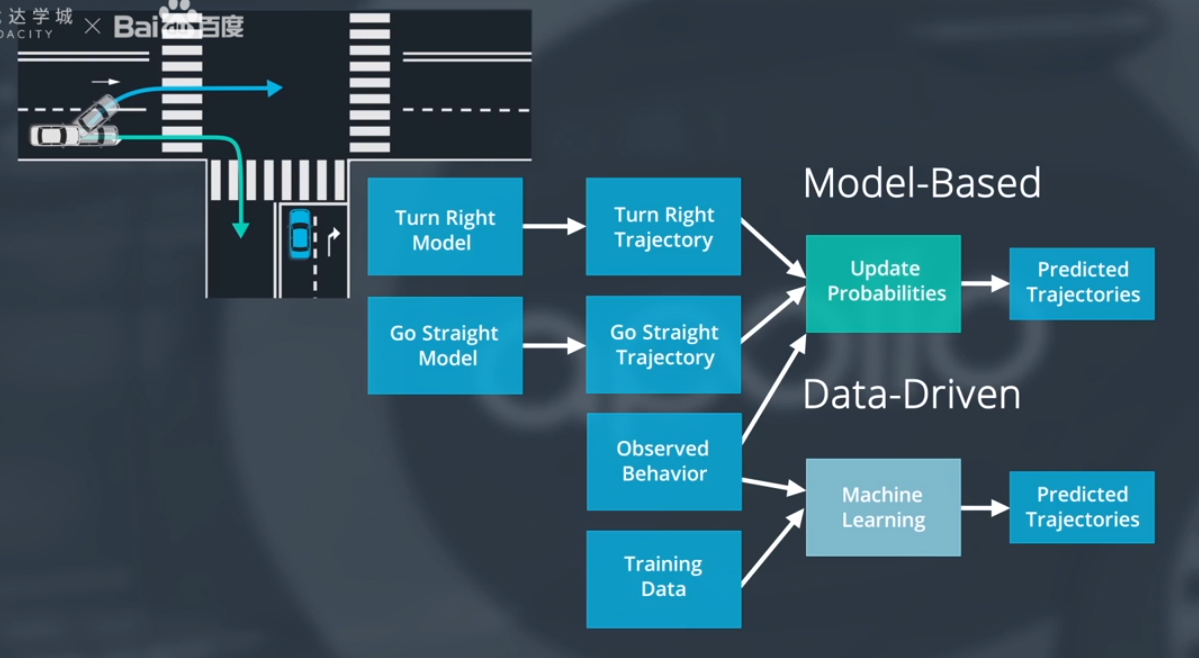
两种不同的预测方式:
- 基于模型的预测
- 构建两个候选的预测模型
- 一个模型描述了进行右转弯,用绿色轨迹表示
- 如果看到车在右转弯车道保持前行,我们会更加倾向于预测对车辆右转
- 另一个模型描述了继续直行,用蓝色轨道表示
- 如果看到车辆开始向左改变车道,我们会更加确信车辆最终会直行
- 数据驱动预测
- 数据驱动预测使用机器学习算法,通过观察结果来训练模型
- 数据驱动方法的优点是训练数据越多,模型效果越好
基于车道序列的预测
将道路分成多个部份
关心车辆在这些区域内如何进行转换
例如直行汽车的运动可以描述为车道序列是 0-1-3-7
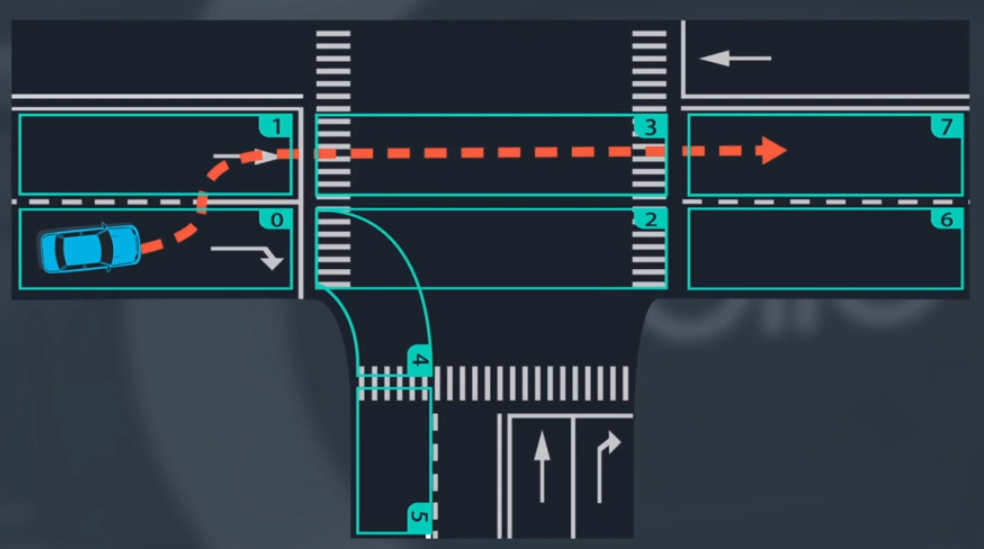
障碍物状态
为了预测一个物体的运动,需要了解到这一个物体的状态,我们需要得知这一个物体的朝向、位置、速度、加速度来预测它将会做什么。
此外预测模块还需要了解到从物体到车道线段边界的纵向和横向距离,以及之前时间间隔的状态信息,来做出更准确的预测。
预测目标车道
- 使用车道序列框架的目标是为道路上的物体生成轨迹。
- 问题从稍微简单一点的开始,我们需要预测车辆在车道线段之间的过渡
- 将复杂的路径预测问题简化为选择问题
- 所构建的模型与车辆状态和车道段作为输入,以车辆可能采用每个车道序列的概率作为输出
- 随着数据以及时间的增加,模型可以自我迭代更新,精度不断提升
递归神经网络
- 递归神经网络RNN是一种利用时间序列数据特征的一种预测方法
- 多层感知网络MLP
- 通过隐藏层提取特征,然后把特征糅合为高级特征,并使用这些特征来进行计算,并得到结果
- 通过比对增值以及预测值将预测误差从后往前传播,修正神经网络的权重,以提高神经网络的准确性。
- 建立像这样的多重结构的递归神经网络称之为 MLP单元
- 从数据序列中提取出高级特征
- 每个单元将序列的一个元素作为输入并预测序列的下一个元素作为输出
- 前每个单元之间都建立一个额外的连接,使得该单元可以了解到前一个单元的预测输出
递归神经网络在目标车道预测的应用
Apollo使用RNN建立一个模型来预测车辆的目标车道:
- 分别为车道序列、相关对象状态提供一个RNN模型,连接这两个RNN的输出并将它们馈送到另一个神经网络
- 该神经网络会估计每个车道序列的概率,具有最高概率的车道序列是我们预测目标车辆将遵循的序列
- 训练时比较网络的输出和真值标记,并使用反向传播算法来训练网络
规划
简介
- 路径规划是指通过一定的规则,找到一条通过世界的路径来达到我们想去的地方。
- 在路线导航时,将地图数据作为输入,并输出可行驶路径。
- 在宏观上构建出路线后,我们需要将轨迹规划释放到微观上
- 轨迹由一系列点定义,每个点都有一个关联速度和一个指示何时应抵达那个点的时间戳
- 路径规划使用三个输入
- 第一个输入为地图,Apollo提供的地图数据包括公路网和实时交通信息
- 第二个输入为我们当前在地图上的位置
- 第三个输入为我们的目的地,目的地取决于车辆中的乘客
世界到图
- 在使用算法进行宏观上的路径规划前,我们需要将地图数据重新格式化为“图形”的数据结构
- 该图形由“节点”(node)和“边缘”(edge)组成
- 节点代表路段
- 边缘代表这些路段之间的连接
- 我们可以对一个节点移动到另一个节点所需的成本进行建模
- 一旦我们在图形中找到了一条好路径,就可以轻松地将图形中的路径重新转换为地图上的路径
路径查找
- A* 是经典的路径查找处理算法
A*的工作原理:
- 我们用变量g和h表示每个成本
- g值为开始节点前往候选节点的成本
- h值为候选节点前往目的地的估计成本或启发式成本
- 对于每个候选节点,我们通过添加g值和h值来计算总和,即f值
- 最佳候选节点是f值最小的节点
- 每当我们抵达新节点时,我们通过重复此过程来选择下一个候选节点
轨迹生成与评估
- 高等级地图路线只是规划过程中的一部分,我们仍需要构建沿这条路线前进的低等级轨迹
- 在某些场景下,我们可能需要与前面掉头的汽车互动、或者希望超过一辆在公路上行驶的慢车,这需要更低级别、更高精确度的规划,我们将这一级别的规划称为轨迹生成。
- 轨迹生成的目标是生成一系列路径点所定义的轨迹
- 每个路径点都有一个时间戳和速度
- 需要保证通过时,每一个路径点未被占用
- 需要对轨迹进行评估:
- 首先轨迹要合理合法
- 其次需要对成本进行评估(使用成本函数),成本由各种犯规处罚组成
- 偏离道路中心,有可能产生碰撞
- 速度限制
- 轨迹的曲率和加速度让乘客感到不舒服
- 轨迹成本将所有这些缺陷聚合为单个数字,对不同的轨迹按数字大小进行排名
- 不同环境下使用的成本函数不一样
Frenet 坐标系
- 在描述车辆位置时,笛卡尔坐标系并不是最佳的选择。
- 因为这样我们不知道路在哪,也很难知道车辆行驶了多远,是否偏离道路中心等
- 笛卡尔坐标系的替代解决方案为Frenet坐标系
- 它描述了汽车相对于道路的位置
- s代表沿道路的距离,也被称为纵坐标
- d表示与纵向线的位移,也被称为横坐标
- 在道路的每个点上,横轴和纵轴都是垂直的
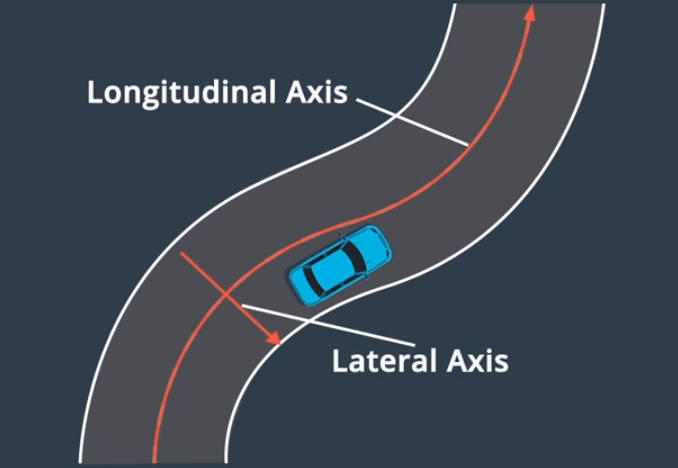
路径-速度解耦规划
路径-速度解耦规划将轨迹规划分为两步:
- 路径规划
- 在路径规划步骤中生成候选曲线,这是车辆可行驶的路径
- 使用成本函数对每条路径进行评估,选择成本最低的路径
- 速度规划
- 确定沿这条路线行进的速度
- 使用优化功能为路径选择受到各种限制的良好速度曲线
- 通过将路径和速度曲线相结合可构建车辆行驶轨迹
路径生成与选择
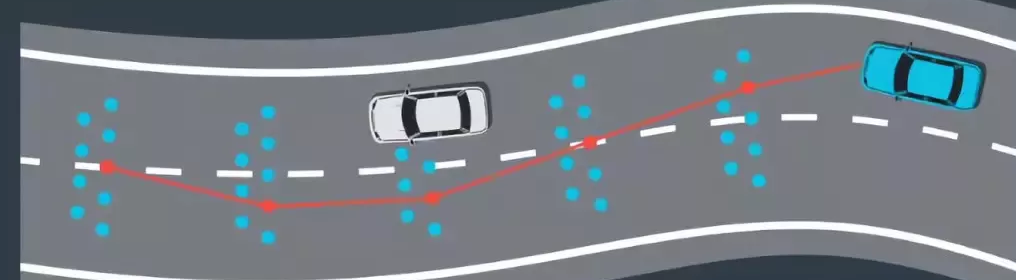
首先将路段分割成单元格
然后对这些单元格中的点进行随机采样
从每个单元格中取一个点并将点连接从而创建候选路径
使用成本函数对这些路径进行评估并选择成本最低的路径
成本因素:
- 与车道中心的偏离
- 与障碍物的距离
- 速度和曲率的变化
- 对车辆的压力
- 或希望列入的任何其他因素
ST图
在ST图中,“s”表示车辆的纵向位移、“t”表示时间
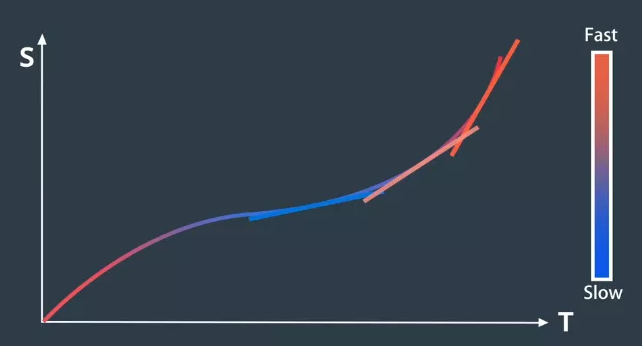
速度规划
- 将 ST 图离散为多个单元格
- 在 ST 图中可以将障碍物绘制为在特定时间段内阻挡道路的某些部分的矩形
- 为避免碰撞,速度曲线不得与此矩形相交
- 使用优化引擎为该图选择最佳的速度曲线
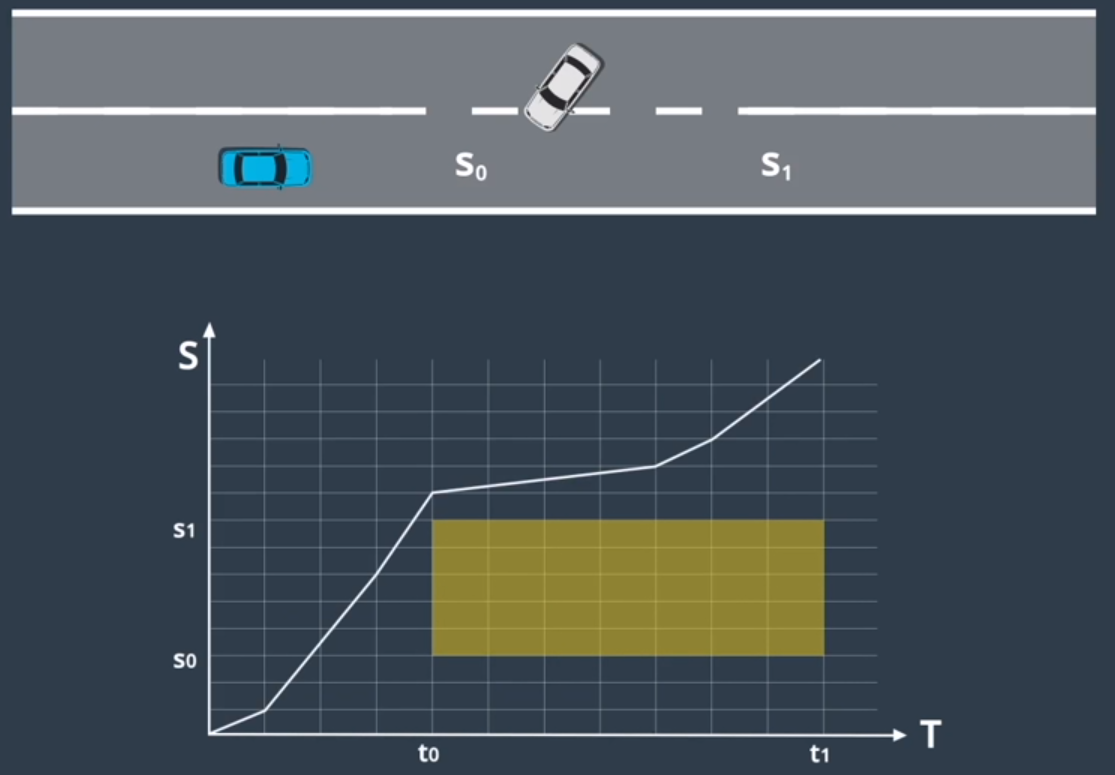
二次规划
- 离散化所生成的轨迹并不平滑
- 使用“二次规划”技术
- 二次规划将平滑的非线性曲线与这些分段式线性段拟合
Lattice 规划
- Lattice 规划是一种轨迹生成方法
- Lattice 规划具有两个步骤即先分别建立 ST 和 SL 轨迹,然后将它们合并为生成纵向和横向二维轨迹
- 相对于纵向轨迹的横向偏移的二维轨迹称之为 SL 轨迹
- 使用成本函数对这些轨迹进行评估并选择成本最低的轨迹
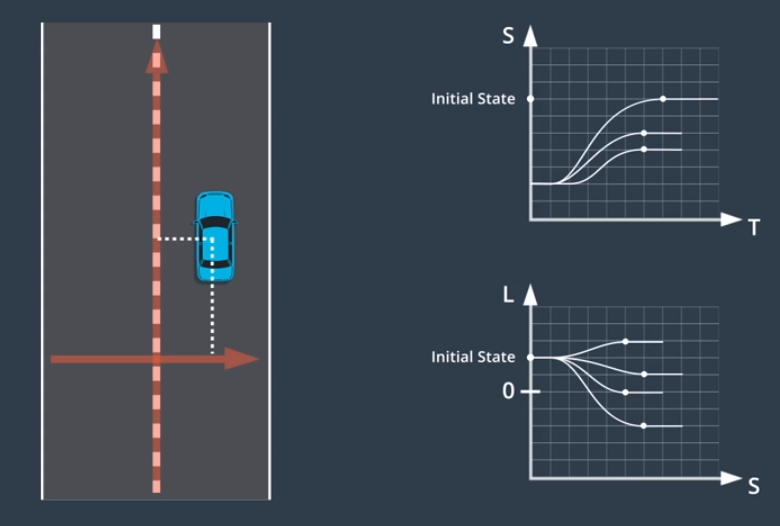
ST轨迹的终止状态
- 巡航
- 巡航意味着车辆将在完成规划步骤后定速行驶
- 对于这种模式,所有最终状态的加速度均为零
- 跟随
- 速度和加速度将取决于要跟随的车辆,在这种模式下,速度和加速度都会进行修正
- 停止
- 需对汽车何时何地停止进行抽样,这里速度和加速度会被修正为 0
SL轨迹的终止状态
- 无论车辆进入怎样的终止状态,车辆都应该稳定地与车道中心线对齐
- 为了达到这种终止状态,车的朝向和位置的一阶和二阶导数都应该为零
Lattice规划的轨迹生成
- 一旦同时拥有了 ST 和 SL 轨迹,就需要将它们重新转换为笛卡尔坐标系。
- 然后可以将它们相结合构建由二维路径点和一维时间戳组成的三维轨迹
- ST 轨迹是随时间变化的纵向位移,SL 轨迹是纵向轨迹上每个点的横向偏移
- 由于两个轨迹都有纵坐标 S,所以可以通过将其 S 值进行匹配来合并轨迹
控制
简介
- 控制是驱使车辆前行的策略。对于汽车而言,最基本的控制输入为转向、加速和制动。通常,控制器使用一系列路径点来接收轨迹。控制器的任务是使用控制输入让车辆通过这些路径点。
控制器的三个要求:
- 准确
- 应避免偏离目标轨迹
- 这对于安全来说,尤为重要
- 可行性
- 现实中汽车向北行驶时,让它立即向东转是无法做到的
- 平稳度
- 舒适的驾驶非常重要,如果车辆行驶得不规律,那乘客永远不会想再次乘坐它了
- 驱动必须是连续的,应避免突然转向、加速或制动
三种可行的控制策略:
- 比例积分微分控制(PID)
- 线性二次调节器(LQR)
- 模型预测控制(MPC)
控制流程
控制器预计有两种输入:目标轨迹与车辆状态
- 目标轨迹
- 目标轨迹来自规划模块,在每个轨迹点,规划模块指定一个位置和参考速度
- 车辆状态
- 车辆状态包括:通过本地化模块来计算的车辆位置、从车辆内部传感器获取的数据(如速度、转向和加速度)
我们使用这两个输入来计算目标轨迹与实际行进轨迹之间的偏差
- 控制器的输出是控制输入(转向、加速和制动)的值
PID 控制
- PID的第一组件为P代表“比例”(Proportional)
- 设想一辆车正试图遵循目标轨迹,P控制器在车辆开始偏离时立即将其拉回目标轨迹。比例控制意味着,车辆偏离越远,控制器越难将其拉回目标轨迹。
- D代表“微分”(Derivative)
- D项致力于使运动处于稳定状态
- 它增加了一个阻尼项,可最大限度地减少控制器输出的变化速度
- 最后一项I代表积分(Integral)
- 该项负责纠正车辆的任何系统性偏差
- 转向可能失准,这可能造成恒定的转向偏移,为解决这一问题,控制器会对系统的累积误差进行惩罚
PID优劣对比
- PID控制器很简单,但它在很多情况下的效果很好
- 但是PID控制器只是一种线性算法,对于非常复杂的系统而言,这是不够的
- 另一个问题在于PID控制器依赖于实时误差测量,这意味着受到测量延迟限制时可能会失效
线性二次调节器
线性二次调节器(Linear Quadratic Regulator 或LQR)是基于模型的控制器,它使用车辆的状态来使误差最小化
Apollo使用LQR进行横向控制
横向控制包含四个组件(称这四个组件的集合为X):
- 横向误差
- 横向误差的变化率
- 朝向误差
- 朝向误差的变化率
三个控制输入(称这个控制输入集合为U):
- 转向
- 加速
- 制动

这个等式是线性的,因为我们用∆x来改变x时,并用∆u来改变u。x点的变化也会让这个等式成立
- LQR中的Q的目标是为了让误差最小化,但我们也希望尽可能少地使用控制输入
- 当车往右转的特别厉害之际,添加到误差总和中。当控制输入将汽车往左侧转时,从控制输入总和中减去一点
- 最优的u应该最小化二次项的和随时间的积分,在数学中我们将这个积分值称为成本函数
模型控制预测
模型预测控制(或MPC)是一种更复杂的控制器,它非常依赖于数学优化,但基本上可以将MPC归结为三个步骤:
- 建立车辆模型
- 该模型近似于汽车的物理特性
- 该模型估计了假如将一组控制输入应用于车辆时会发生什么
- 使用优化引擎计算有限时间范围内的控制输入
- 通过搜索密集数学空间来寻求最佳解决方案
- 为缩小搜索范围,优化引擎依赖于车辆模型的约束条件
- 为使乘客感觉更舒适,对控制输入的调整应该很小,因为动作变化幅度过大会让乘客感到不舒服
- 执行第一组控制输入
总结
- PID控制是一种简单而强大的控制算法
- 线性二次调节器和模型预测控制是另外两种类型的控制器,它们更复杂,但也更强大、更准确